Introduction

Dendrimers are multi-branched macromolecules of nanometric size. Dendrimers consist of three distinct elements as a central core and an inner surface with a dendritic structure consisting of branches, with external surface groups, see Figure 1 [1]. There is a powerful exclusivity among the molecular structures of chemical compounds and their chemical properties. Topological indices which are also called molecular descriptors are numerical quantities associated with a graph used to predict the physicochemical features of chemical structures such as melting, boiling, flash points, enthalpy of vaporization, etc. [2, 3]. Among algebraic Polynomials, M-Polynomial was expressed by Klavzar and Deutsch [4] and has a fundamental role in specifying the formula of topological indices based on the degree [5]. M-polynomial helps to find several topological indices based on the degree, such as the first and second Zagreb, modified second Zagreb [6], symmetric division [7], generalized Randić [8], inverse Randić inverse sum [8], harmonic, and augmented Zagreb indices [4, 9]. In primary definitions, see [10, 11]. Table 1 presents some topological indices based on the degree derived from M-polynomial [4, 12]. Throughout this article, all graphs are simple and connected. We denote the degree of the vertex v with, the vertices, and edges set of graph G with V(G) and E(G) respectively, and the number of edges in G with e(G). Likewise, we use the following formula, which is well known as the degree-sum formula [13].

Materials and Methods

In this article, M-polynomials of Porphyrin-cored dendrimers of the  generation of the first, second, third, and fourth type are calculated. Using these M- Polynomials, several topological indices based on the obtained degree. Combinatorial computations with the technique of counting the degree of vertices and the method of partition edges have been applied to obtain the results. Then, using these partitions, the form of the M-polynomial of Porphyrin-cored dendrimers is obtained. Furthermore, the surface of the M-polynomial is plotted using Maple 2022.

Definition 1 [5]. A loop is an edge whose terminal vertices are equal. Multiple edges are edges with the same terminal vertices. A simple graph does not have loops and multiple edges.

Definition 2 [5]. A graph G is Connected, whenever there is a path among both vertices.

Definition 3 [5]. The M-polynomial of graph G is introduced as follows:

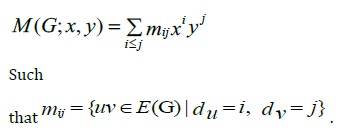
Results and Discussion

Porphyrin-cored dendrimer- I (PCD-I)

Our first molecular diagram is PCD-I of generation  with n ⩾ 1 growth stage [3]. The PCD-I is composed of 2 branches, with one core at its centre. The central core comprises 25 vertex and 34 edges, as depicted in Figure 2. According to Table 2 and by degree-sum formula, the total number of edges in PCD-I is 4×2ⁿ +30 [3].

In Figure 3, according to the degrees of vertices incident with each edge, a set of edges PCD-I can be partitioned into 5 categories. We compute their cardinalities in Table 3.

Porphyrin-cored dendrimer-II (PCD-II)

Our second molecular diagram is PCD-II of generation    with n ⩾ 1 growth stage. PCD-II is composed of four similar branches, such that one core is at its center. The central core is composed of 25 vertex and 36 edges, as displayed in Figure 5. According to Table 4 and by degree-sum formula, the total number of edges in PCD−II is 8 × 2ⁿ + 28 [3].

In Figure 5, according to degrees of the vertex incident with each edge, set of edges PCD−II can be partitioned into 5 categories. We compute their cardinalities in Table 5.

Porphyrin-cored dendrimer- III (PCD-III)

Our third molecular diagram is PCD−III of generation  with n ⩾ 1 growth stage. PCD−III is composed of 25 vertex and eight similar branches, such that one core is at its center, as demonstrated in Figure 8. The central core is composed of 25 vertices and 40 edges, as illustrated in Figure 8. According to Table 6 and by degree-sum formula, the total number of edges in PCD−III is 16 × 2ⁿ + 24 [3].

In Figure 8, according to the degrees of the vertex incident with each edge, a set of edges PCD-III can be partitioned into 4 categories. We compute their cardinalities in Table 7.

Proposition 6. Let PCD-III be the Porphyrin-cored dendrimer of the third type of generation with n ⩾ 1 growth stage. Then,

Conclusion

According to Figures 4, 7, 10, and, 13, all diagrams are exponential functions with base 2, and they are increasing with the increase in the number of generations. In dendrimers PCD-I, PCD-II, and PCD-IV, the Augmented Zagreb index value is the highest, and the Second Modified Zagreb index value is the lowest, while in PCD−III, up to the 3^rd generation, the Symmetric Division Index value is the highest. In all four types of porphyrin-cored dendrimers, the numerical values of the General Randi and the Harmonic indices almost are very close to each other. In PCD-I, in the higher generations, the First Zagreb and the Second Zagreb indices, and also the Inverse Randi and Symmetric Division indices, coincide. Figures 3, 6, 9, and, 12 show that amounts computed using M-Polynomial have various behaviors related to parameters of x and y. The results obtained in this article will help researchers to observe the strong correlation between the physicochemical properties of dendrimers and topological indices in the study of drugs.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Authors' contributions

All authors contributed to data analysis, drafting, and revising of the paper and agreed to be responsible for all the aspects of this work.

Conflict of Interest

We have no conflicts of interest to disclose.

Orcid

Mehri Hasani

https://orcid.org/0000-0002-3970-2339

Masoud Ghods

https://orcid.org/0000-0002-5006-5107

HOW TO CITE THIS ARTICLE

Mehri Hasani, Masoud Ghods. M-Polynomials and Topological Indices of Porphyrin-Cored Dendrimers. Chem. Methodol., 2023, 7(4) 288-306

DOI: https://doi.org/10.22034/CHEMM.2022.370497.1626

URL: http://www.chemmethod.com/article_164594.html